Navigation
Sie sind hier:
Startseite
![]() Archiv
Archiv
![]() 2004/05 2. Halbjahr
2004/05 2. Halbjahr
![]() Känguru der Mathematik
Känguru der Mathematik
Siehe auch
111 Schülerinnen und Schüler des TGG aus 14 Klassen und dem Leistungskurs Mathematik haben am diesjährigen internationalen Känguru-Wettbewerb teilgenommen.

Teilnehmer aus den Jahrgängen 5 und 6 mit Barbara Hallerbach
Der 1978 in Australien ins Leben gerufene Wettbewerb breitet sich in der ganzen Welt aus. 80% der Secondary Schools Australiens nehmen jährlich an dem „Australian Mathematics Competition" teil. 1994 gelangte der Wettbewerb nach Frankreich und 1995 beteiligten sich in Deutschland die ersten Schülerinnen und Schüler an diesem Test.
Ihr wollt bestimmt wissen, warum der Test Känguru-Wettbewerb heißt? Das könnt ihr unter www.mathe-kaenguru.de erfahren.
In diesem Jahr beteiligten sich 4.100 Schulen, insgesamt 334.217 Schülerinnen und Schüler. 30 Aufgaben waren zu lösen. Der Schwierigkeitsgrad ist nach Klassenstufen gestaffelt. In allen Alterstufen ist die maximale Punktzahl 150.
Hier die erfolgreichen Gewinnerinnen und Gewinner des TGG:
| Yannick Behrends | 5e | 131,25 Punkte |
| Riekje Kück | 6a | 125,00 Punkte |
| Simon Boomgaarden | 8en | 112,50 Punkte |
| Stefan Gustke | 9en | 93,25 Punkte |
| Tammo Lossau | 10en | 112,50 Punkte |
| Benjamin Becker | LK Mathematik | 83,25 Punkte |
Herzlichen Glückwunsch!
Wollt ihr wissen, wie Aufgaben aus diesem Test aussehen?
(Hinweis: Nur eine Antwort ist richtig!!)
Laure hat 2004 Murmeln, von denen die Hälfte grün und ein Drittel gelb ist. Wie viele Murmeln haben andere Farben?
Die vier in der Zeichnung abgebildeten Kreise sind gleich groß. Die drei äußeren Kreise, deren Mittelpunkte die Eckpunkte eines gleichseitigen Dreiecks sind, berühren den inneren Kreis. Das Verhältnis des Flächeninhalts der grauen Fläche zum Flächeninhalt der schraffierten Fläche beträgt
Die Summe der Punkte auf den einander gegenüberliegenden Seiten eines Würfels sei stets 7. Der Würfel rollt wie in der Abbildung dargestellt.
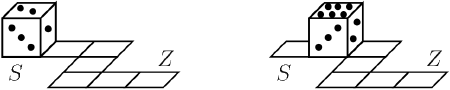
Im Startpunkt S liegt die 2 oben. Welche Zahl ist im Endpunkt Z oben?
Mama Känguru und ihr Sprössling Jumpy trainieren in einem Stadion mit einer Bahnlänge von 330 m für ein Wettspringen. Gleichzeitig springen sie an der Startlinie los, jder macht einen Sprung pro Sekunde, Jumpys Sprünge sind je 1,5 m, die der Mama je 3,5 m weit. Nach einer Minute gibt Jumpy auf und bleibt sitzen, die Mama springt unbeirrt weiter. Wie lange braucht sie, bis sie Jumpy wieder erreicht?
Weitere Aufgaben könnt ihr bei den Mathematiklehrerinnen und Mathematiklehrern erhalten. Viel Spaß beim Denken.
Wollt ihr beim nächsten Mal mitmachen? Der Termin für den Wettbewerb 2006 steht schon fest:
16. März 2006
Text: B. Hallerbach; Foto: A. Dietz-Schatt
2005-07-08, bo