Sie sind hier:
Startseite
> TGG
>
TGG
> Lehrpläne
>
Lehrpläne
> Mathematik
Mathematik
-
-
-
Rückwärtsschließen im Baumdiagramm
- Umkehrung der Blickrichtung im Baumdiagramm
- vereinfachte Bayes-Formel
- Mehrfachanwendung
-
Ähnlichkeit
- Ähnlichkeit, zentrische Streckung, Strahlensatzfiguren
- Muster erzeugen durch Ähnlichkeitsabbildungen
- senkrechte Achsenstreckungen
-
Rund um die Parabel
- Parabel als Ortskurve und als Funktionsgraph
- Abbildungen
- Extremal- und Schnittprobleme, quadratische Gleichungen
-
Zahlbereichserweiterung II: Wurzeln und ihre Dezimaldarstellungen
- Näherungswerte für Wurzeln
- Umformung einfacher Wurzelterme
- Irrationalität, Vergleich von ℚ und ℝ
-
Von der Konstruierbarkeit zur Berechenbarkeit
- Satzgruppe des Pythagoras
- trigonometrische Beziehungen am rechtwinkligen Dreieck
- Anwendungen in Ebene und Raum
-
-
Bernoulliketten und Alternativtests
- Bernoulli-Experimente und Abzählverfahren, Wahrscheinlichkeiten
- Simulation mit Zufallsziffern oder Galton-Brett
- Alternativtests und Fehler
-
Gleichungslöseverfahren
- Gleichungen aus inner- oder außermathematischen Problemen
- Tabellarische, graphische, symbolische Lösungsverfahren
- ein iteratives Lösungsverfahren
-
Längen, Flächeninhalte, Rauminhalte und Näherungsverfahren
- π, Formeln für Kreis und Kreisteile
- Zylinder, Pyramide, Kegel, Kugel und Teilkörper
- Termumformungen
-
Kreisgleichungen und Kreisfunktionen
- Kreis in Parameter- und Koordinatendarstellung
- Sinus- und Kosinusfunktion, Bogenmaß
- Parametervariationen
-
Wachstumsmodelle
- Modellierung von Wachstumsprozessen, iterativ und explizit
- lineares, exponentielles, beschränktes Wachstum
- Potenzen, Potenzfunktionen, Exponentialfunktionen
-
-
-
Prognosen und mehrstufige Zufallsexperimente
- Durchführen und Auswerten von Zufallsexperimenten
- Prognose, relative Häufigkeit, Wahrscheinlichkeit als Voraussage über die relative Häufigkeit
- Verbesserung der Prognose durch Erkenntnisgewinn
- Empirisches Gesetz der großen Zahlen (propädeutisch)
- Eigenschaften der relativen Häufigkeit / Wahrscheinlichkeit
- Berechnen von Wahrscheinlichkeiten
- Laplace-Wahrscheinlichkeit als Sonderfall
- Klassische Zufallsexperimente (Münze, Urne, Würfel, Glücksrad)
- Mehrstufige Zufallsexperimente
- Ereignisse
- Darstellung mittels Baumdiagramm
- Strukturierendes Arbeiten: zielgerichtete Reduktion auf das Wesentliche (reduziertes Baumdiagramm)
- Modellbildung (Ziehen mit und ohne Zurücklegen)
- Pfadregeln – Rechnen mit Wahrscheinlichkeiten
- Multiplikationsregel
- Additionsregel
-
Längen, Flächen, Rauminhalte und deren Terme
- Berechnung von Umfang bzw.
Gesamtkantenlänge Flächeninhalt bzw.
Oberflächeninhalt und Rauminhalt an Polygonen und Polyedern
- Geometrische Sachverhalte durch Terme beschreiben
- Terme geometrisch interpretieren (binomische Formeln u. a.)
- Prüfung der Äquivalenz von Termen durch geometrische
Interpretation und durch exemplarisches Einsetzen von Zahlen
- Nachweis der Äquivalenz durch Umformung der Terme mithilfe der Rechengesetze
- Kontextfreie Termumformungen (Ausmultiplizieren und Ausklammern)
-
Ähnlichkeit
- Ähnliche Dreiecke
- Verhältnisgleichungen
- Berechnung von Streckenlängen
- Heuristische Strategie: Suche nach ähnlichen Figuren
- Ähnlichkeitssätze für Dreiecke und ihre Anwendung
- Zentrische Streckung und ihre Eigenschaften
-
Quadratische Funktionen und ihre Graphen
- Parabel als Graph einer quadratischen Funktion
- Normalparabel und deren Abbildungen durch Verschiebung und senkrecht-affine Streckung
- Parametervariation bei
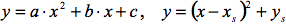
- Anwendungen und Modellierungen: Optimierungs- und Schnittprobleme
- Lösen quadratischer Gleichungen
- Tabellarisch, grafisch, symbolisch und mithilfe eines Gleichungslösers
-
-
Von der Konstruierbarkeit zur Berechenbarkeit
- Satzgruppe des Pythagoras mit Beweisen
- Umkehrung des Satzes von Pythagoras
- Sinus, Kosinus, Tangens in rechtwinkligen Dreiecken
- Tangens als Steigungsmaß
- Suche nach rechtwinkligen Dreiecken als heuristische Strategie
- Berechnung an Dreiecken, ebenen und räumlichen Figuren
- Anwendungsprobleme aus verschiedenen Bereichen
-
Zahlenbereichserweiterung II: Wurzeln und ihre Dezimaldarstellungen
- Dezimaldarstellungen von Quadratwurzeln mit einem iterativen verfahren,
z. B. Heronverfahren oder Intervallhalbierungsverfahren
- Rechnen mit Näherungswerten und Rechengesetze in ℝ
- Einfache Umformungen mit Wurzeltermen
- Begründung der Irrationalität oder Inkommensurabilität
- Qualitativer Vergleich von ℚ und ℝ
-
Längen, Flächeninhalte, Rauminhalte und Näherungsverfahren
- Bestimmung von π
- Herleitung der Formeln für Flächeninhalt und Umfang eines Kreises
- Entwickeln mindestens einer Volumenformel
- Berechnungen an Zylinder, Pyramide, Kegel und Kugel
- Berechnungen von einfachen Teilfiguren und Teilkörpern
- Abschätzung der Maßzahlen unregelmäßiger Körper
-
Periodizität und Kreisfunktionen
- Graphen der Sinus- und Kosinusfunktion
- Beschreibung des Einheitskreises durch Sinus- und Kosinusfunktion
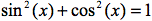
- Bogenmaß
- Modellierung periodischer Vorgänge
- Parametervariationen für trigonometrische Funktionen vom Typ
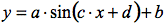
-
-
Bernoulliketten
- Bernoulliexperimente und Bernoulliketten
- Anzahl der Wege im Baumdiagramm mit genau k Treffern
- Binomialkoeffizient
- Pascaldreieck
- Simulation mit Zufallsziffern oder Galton-Brett
- Wahrscheinlichkeiten in Bernoulliketten
-
Wachstumsmodelle
- Iterative Modellierung von Wachstumsprozessen
- Tabellarisch, grafisch, symbolisch
- Exponentielles Wachstum
- Explizite Beschreibung
- Umkehrprobleme (z. B. Verdoppelungs- und Halbierungsprobleme)
- Logarithmen
- Beschränktes Wachstum
- Propädeutischer Grenzwertbegriff
- Potenzen mit Exponenten aus ℚ
- Potenzgesetze
- Potenzfunktionen
- Exponentialfunktionen
-
Ableitung, Ableitungsfunktion
- Ableitung, Deutung der Ableitung als lokale Änderungsrate und als Tangentensteigung
- Begriff der Ableitungsfunktion
- Ableitungsfunktionen von ganzrationalen Funktionen
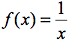 ,
,
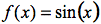
- Regeln zur Berechnung der Ableitungsfunktionen
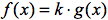 ,
,
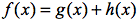
- Anwendung der Ableitung auf gegebene Funktionen
- Zusammenhang zwischen dem Graphen der Funktion und dem der Ableitungsfunktion
-
Funktionsuntersuchungen und Anwendungen
- Untersuchungen von ganzrationalen Funktionen bis vierten Grades und ihren Graphen
- Anwendungen: Extremwertaufgaben mit Nebenbedingungen
-
Im Frühjahr 2007 wird es eine zentral gestellte Vergleichsarbeit in Mathematik geben.
Die besonders zu berücksichtigenden Kompetenzen:
- Mathematisch argumentieren
- Probleme mathematisch lösen
- Mathematisch modellieren
- Mathematische Darstellungen verwenden
- Mit symbolischen, formalen und technischen Elementen der Mathematik umgehen
- Kommunizieren
Die besonders zu berücksichtigenden Kompetenzen:
- Leitidee Zahl
- Leitidee Messen
- Leitidee Raum und Form
- Leitidee funktionaler Zusammenhang
- Leitidee Daten und Zufall
-
-
Klasse 5
Kreis und Winkel
- Kreise
- Winkel
- Koordinatensysteme
Natürliche Zahlen
- Darstellungsformen
- Zahlenmenge ℕ
- Zahlterme
- Beziehungen von Rechenoperationen untereinander
Körper und Figuren
- In unserer Umwelt Modelle beschreiben und zeichnen
- Zerlegen und zusammenfügen
Längen-, Flächen- und Rauminhalte
- Längen-, Flächen- und Raummaße
- Zehner- und Dezimalbrüche
- Größen runden, vergleichen
- Rechtwinklige geometrische Figuren und Körper
Bruchzahlen I
- Grundvorstellungen entwickeln
- Vergleichen und Ordnen
Daten
- Daten sammeln
- Daten erstellen
- Daten auswerten
Bruchzahlen II
- Prozente
- Mischungsverhältnisse
- Maßstäbe
- Darstellungsformen
-
Klasse 6
Symmetrien erkennen und erzeugen
- Parkettierungen
- Muster erzeugen und analysieren
- Kongruenzabbildungen
Rechnen mit Bruchzahlen
- Grundrechenarten mit einfachen Bruchzahlen
Prognosen
- Durchführen und Auswerten von Zufallsexperimenten
- Berechnen von Wahrscheinlichkeiten
Rationale Zahlen
- Negative Größen
- Zahlbereichserweiterung
- Rechenoperationen
- Rechengesetze
Proportionalitäten
- Zuordnungen
- Proportionale und antiproportionale Zuordnungen
- Dreisatz
- Prozentrechnung
- Zinsrechnung
-
Klasse 7
Dreiecke und Vierecke
- Besondere Linien im Dreieck
- Verschiedene Ortslinien
Terme und Gleichungen
Berechnungen an Vielecken und Prismen
- Umfang und Flächeninhalt geradlinig begrenzter Figuren
- Oberfläche und Volumen von Prismen
- Schrägbilder und Netze
- Maßstabsgetreue Konstruktionen
Mehrstufige Zufallsexperimente
- Baumdiagramm
- Multiplikationsregel
- Additionsregel
Lineare Funktionen
- Tabelle, Graph
- Sachtexte
- Lineare Funktionen identifizieren und klassifizieren
- Darstellungen durch Terme und Gleichungen
- Wechsel: Term – Gleichung – Tabelle – Graph
- Modellierung von Sachsituationen
- Steigung als konstante Änderungsrate
-
Klasse 8
Terme und Gleichungen mit Klammern
- Lineare Gleichungen mit zwei Variablen
- Lineare und quadratische Gleichungen
- Lineare Gleichungssysteme mit zwei Variablen
- Lösbarkeit von Linearen Gleichungssystemen
Quadratwurzeln – Reelle Zahlen
- Notwendigkeit der Zahlbereichserweiterung
- Näherungsverfahren: z. B. Heron-Verfahren
- Unterscheidung rationale Zahl – irrationale Zahl
- Einfache Rechenaufgaben
Satz des Pythagoras
Parabeln – Quadratische Funktionen und quadratische Gleichungen
- Tabelle, Graph
- Sachtexte
- Quadratische Funktionen identifizieren und klassifizieren
- Darstellung durch Terme und Gleichungen
- Wechsel: Term – Gleichung – Tabelle – Graph
- Modellierung von Sachsituationen
- Parabel als Ortslinie
Daten
- Datenpaare grafisch darstellen
- Lineare und quadratische Regression
![]() TGG
TGG
![]() Lehrpläne
Lehrpläne
![]() Mathematik
Mathematik