Zum Inhalt springen

Seiteninhalt

Siehe auch

Sie sind hier: Startseite > TGG > Lehrpläne > Mathematik > Oberstufe

Unterrichtsinhalte im Fach Mathematik – Oberstufe

  1. Jahrgang 11

    • Folgen und Reihen bis zum Grenzwertbegriff
    • Ableitung
    • Ableitungsfunktionen
    • Regeln zur Berechnung der Ableitungsfunktionen
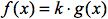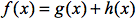
      Formel,
      Formel
    • Untersuchung von Funktionen und ihren Graphen
    • Bestimmung von ganzrationalen Funktionen mit vorgegebenen Eigenschaften
    • Beschreibung von Wachstums- und Zerfallsprozessen mithilfe von Folgen
    • Grundlagen der Stochastik
      • Baumdiagramme und Pfadregeln
      • Bedingte Wahrscheinlichkeit
      • Erwartungswert
      • Bernoulli Versuch
      • Binomialkoeffizient und Fakultät
      • Binomialverteilung

  2. Kursstufe/Jahrgänge 12 und 13

    1. Kurse mit grundlegendem Niveau

      • 12/1: Stochastik
      • 12/2: Analysis
      • 13/1: Analytische Geometrie
      • 13/2: Vertiefung der bisherigen Themen im Prüfungskurs – in anderen Kursen sind auch andere Themen möglich

    2. Kurse mit erhöhtem Niveau

      • 12/1: Analysis
      • 12/2: Analytische Geometrie
      • 13/1: Stochastik
      • 13/2: Vertiefungen

  3. Schwerpunktthemen für das Zentralabitur 2008

    1. Erhöhtes Anforderungsniveau

      • Vertiefungen in Stochastik

        • Wahrscheinlichkeitsverteilungen stetiger Zufallsgrößen, speziell Normalverteilung
        • Vergleich von diskreten und stetigen Wahrscheinlichkeitsverteilungen
        • Hypothesentests (einseitig, zweiseitig) auch für normalverteilte Zufallsgrößen

      • Vertiefung in Analysis

        • Wurzelfunktionen
        • Differenzierbarkeit und Stetigkeit
        • Rotationsvolumina
        • Modellierungen insbesondere mit Wurzelfunktionen

      • Vertiefung in analytischer Geometrie

        • Erstellen und Interpretieren unterschiedlicher Formen von Ebenengleichungen
        • Klassifikation von Geraden- und Ebenenscharen sowie deren gegenseitiger Lagebeziehung
        • Flächen- und Rauminhalte einfacher geometrischer Gebilde wie Dreieck, Viereck, Spat und Pyramide
        • Vektorprodukt mit Anwendungen
        • Metrische Größen in Abhängigkeit eines Parameters
        • Abstandsuntersuchungen unter funktionalen Gesichtspunkten

    2. Grundlegendes Anforderungsniveau

      • Vertiefungen in Stochastik

        • Grundkenntnisse der beschreibenden Statistik – Daten beschreiben und auswerten
        • Unterschied bei der Modellierung „Ziehen aus einer Urne mit/ohne Zurücklegen“
        • Vergleich von Binomialverteilung und hypergeometrischer Verteilung
        • Alternativtest bei binomialverteilter Zufallsgröße

      • Vertiefung in Analysis

        • Gebrochen-rationale Funktionen und deren lokale Näherungen durch ganzrationale Funktionen („Taylornäherung“)
        • Funktionenscharen
        • Ortslinien
        • Modellierungen insbesondere mit gebrochen-rationalen Funktionen

      • Verteifung in analytischer Geometrie

        • Normalenform
        • Abstandsbestimmungen (einschließlich windschiefer Geraden)
        • Flächen- und Rauminhalte einfacher geometrischer Gebilde wie Dreieck, Viereck, Quader und Pyramide
        • Problemstellungen mit Parametern (insbesondere bei Bearbeitung von Gleichungssystemen)

  4. Schwerpunktthemen für das Zentralabitur 2009

    1. Kurse mit erhöhtem Anforderungsniveau

      • Stochastik

        • Grundkenntnisse der beschreibenden Statistik – Daten beschreiben und auswerten
        • Regression; Bestimmung und Interpretation des Korrelationskoeffizienten
        • Vergleich von Binomialverteilung und hypergeometrischer Verteilung
        • Vertrauensintervalle für nicht bekannte Wahrscheinlichkeiten
        • Wahrscheinlichkeitsverteilung stetiger Zufallsgrößen, speziell Normalverteilung

      • Analysis

        • Gebrochen-rationale Funktionen und deren lokale Näherungen durch ganzrationale Funktionen („Taylornäherung“)
        • Abschnittsweise definierte Funktionen; Stetigkeit und Differenzierbarkeit
        • Funktionenscharen
        • Modellierungen insbesondere mit gebrochen-rationalen Funktionen

      • Analytische Geometrie

        • Erstellen und Interpretieren unterschiedlicher Formen von Ebenengleichungen
        • Klassifikation von Geraden- und Ebenenscharen sowie deren gegenseitiger Lagebeziehung
        • Flächen- und Rauminhalte einfacher geometrischer Gebilde wie Dreieck, Viereck, Spat und Pyramide
        • Vektorprodukt mit Anwendungen

    2. Kurse mit grundlegendem Anforderungsniveau

      • Stochastik

        • Grundkenntnisse der beschreibenden Statistik – Daten beschreiben und auswerten
        • Regression; Bestimmung und Interpretation des Korrelationskoeffiezienten
        • Vergleich von Binomialverteilung und hypergeometrischer Verteilung
        • Vertrauensintervalle für nicht bekannte Wahrscheinlichkeiten

      • Analysis

        • Gebrochen-rationale Funktionen und deren lokale Näherungen durch ganzrationale Funktionen („Taylornäherung“)
        • Ortslinien
        • Funktionenscharen
        • Modellierungen insbesondere mit gebrochen-rationalen Funktionen

      • Analytische Geometrie

        • Normalenform
        • Vektorprodukt mit Anwendungen
        • Flächen- und Rauminhalte einfacher geometrischer Gebilde wie Dreieck, Viereck, Quader und Pyramide

  5. Schwerpunktthemen für das Zentralabitur 2010

    1. Kurse mit erhöhtem Anforderungsniveau

      • Stochastik

        • Bedingte Wahrscheinlichkeiten (Berechnung mithilfe von Baumdiagrammen, Vierfeldertafeln oder der Formel von Bayes)
        • Vertrauensintervalle für nicht bekannte Wahrscheinlichkeiten
        • Wahrscheinlichkeitsverteilung stetiger Zufallsgrößen, speziell Normalverteilung

      • Analysis

        • Scharen von gebrochen-rationalen Funktionen
        • Ortslinien
        • Exponentialfunktionen mit Anwendungsbezug

      • Analytische Geometrie

        • Anwendungen von Matrizen bei mehrstufigen Prozessen: Populationsentwicklung, Käufer- und Wahlverhalten, zyklisches und stationäres Verhalten

    2. Kurse mit grundlegendem Anforderungsniveau

      • Stochastik

        • Bedingte Wahrscheinlichkeiten (Berechnung mithilfe von Baumdiagrammen, Vierfeldertafeln oder der Formel von Bayes)
        • Vertrauensintervalle für nicht bekannte Wahrscheinlichkeiten

      • Analysis

        • Scharen von ganzrationalen Funktionen
        • Ortslinien
        • Exponentialfunktionen mit Anwendungsbezug

      • Analytische Geometrie

        • Matrizen im Anwendungsbezug: Materialverflechtungen (Verflechtungsdiagramme, Verflechtungsmatrizen)

2008-02-02, sh